Los ángulos miden una inclinación. Por ejemplo, piensa en la famosa “Torre de Pisa” esta construcción es conocida por estar inclinada.
Para comprender el concepto de ángulo a partir de este ejemplo observa el siguiente dibujo. En este están representados el nivel del piso y la torre con dos segmentos de recta. El ángulo es la medida de inclinación de una recta sobre otra, que en este caso, representa a la inclinación de la torre sobre el piso.

Fue el matemático griego Euclides el primero en plantear una definición para un ángulo y lo hizo así:
“Un ángulo es la inclinación de dos líneas que se encuentran en un plano.”
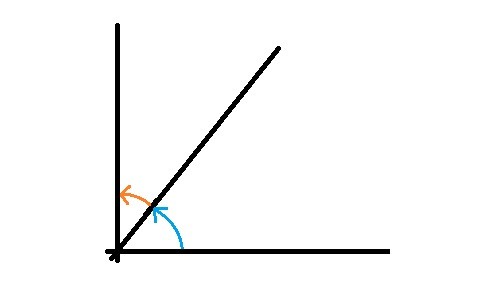
Frecuentemente se representa con una flecha curva al ángulo en cuestión. Los segmentos de rectas que forman los ángulos se llaman lados y el punto donde se encuentran vértice.

Los ángulos se pueden medir con dos unidades distintas: los grados y los radianes.
¿Y qué es un grado? Para entenderlo imagina un reloj con manecillas en el que ambas manecillas apuntan a las 12. Si observas este reloj por transcurso de una hora y 5 minutos, podrás ver que el ángulo entre las manecilla aumenta hasta que las manecillas vuelven a encontrarse poco despues de la 1:05.

Ahora, mentalmente, divide al ángulo que se forma dando un giro completo (marcado en la figura de arriba) en 360 partes iguales, es decir, en 360 pequeños giros, esta medida se le conoce como ángulo y se denota con el símbolo °. Así como 100 centímetros forman un metro, 360 grados forman un giro completo. A la medida de un ángulo también se conoce como amplitud.
Tipos de ángulos
Los ángulos se pueden clasificar de acuerdo a diferentes características.
| Nombre | Amplitud | Dibujo |
|---|---|---|
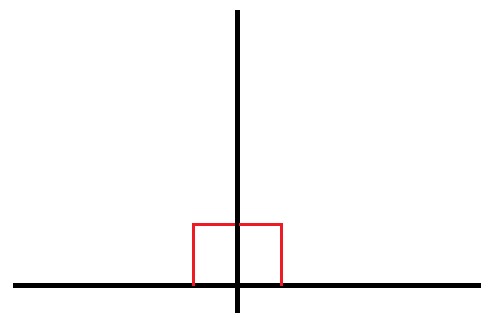
| Ángulo recto | 90º |
|
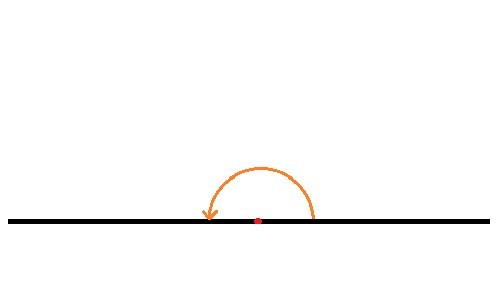
| Ángulo llano | 180º |
|
| Ángulo agudo | Mayor que 0º y menor que 90º |
|
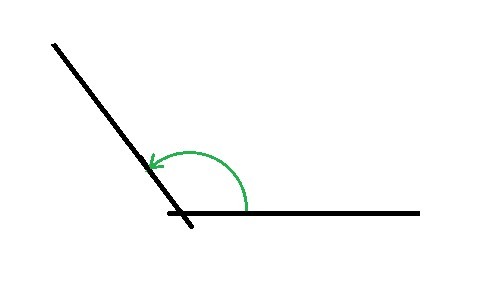
| Ángulo obtuso | Mayor que 90º y menor que 180º |
|
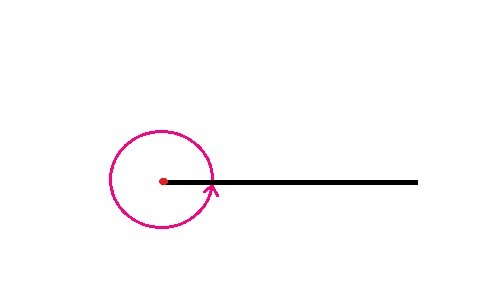
| Ángulo completo | 360º |
|
| Ángulo convexo | mayor que 0º y menor que 180º |
|
| Ángulo cóncavo | mayor que 180º |
|
Otra manera de clasificarlos es por la relación que tiene respecto a otros ángulos, ya sea por su posición, por sus componentes o por la suma entre ellos.
| Nombre | Características | Ejemplo |
|---|---|---|
| Ángulos complementarios | La suma de sus amplitudes es un ángulo recto |
|
| Ángulos suplementarios | La suma de sus amplitudes es un ángulo llano |
|
| Ángulos conjugados | La suma de sus amplitudes es un ángulo completo |
|
| Ángulos consecutivos | Ángulos que tienen un vértice y un lado en común |
|
| Ángulos adyacentes | Son ángulos consecutivos y suplementarios a la vez |
|
Ejemplos
Podemos encontrar ángulos en muchas situaciones de la vida cotidiana, como en las siguientes imágenes.




Ejercicios sobre ángulos (con respuestas):
1) Determina qué tipo de ángulo es el formado por las rectas en color rojo en la siguiente fotografía.

2) Determina a qué tipo de ángulo corresponde el ángulo marcado a continuación.

3) ¿Qué son los ángulos marcados en verde y amarillo (por la relación entre ellos)?

4) Si a y b son dos ángulos suplementarios, y a mide 72 grados ¿Cuánto mide b?
Vea también: