Leyes de los exponentes

Las leyes de los exponentes son las reglas a seguir para realizar operaciones con potencias. La potencia de un número es el resultado de multiplicar ese número por sí mismo más de una vez. Al número se le llama base, y las veces que se multiplica es el exponente, que se coloca en pequeño arriba y a la derecha de la base.

aⁿ = base ^exponente

1) Potencia con exponente cero y base diferente de cero

Todo número con exponente 0 (es decir, elevado a cero) es igual a 1.

Por ejemplo:

a⁰ = 1
2⁰ = 1
15⁰ = 1

2) Potencia con exponente igual a uno

Todo número con exponente 1 es igual a sí mismo. Ejemplos de ello serían los siguientes:

a¹ = a
10¹ = 10
15¹ = 15

3) Producto de potencias de igual base

Para multiplicar potencias de la misma base, se suman los exponentes, como, por ejemplo:

a³ . a⁵ = (a . a . a)(a . a . a . a . a) = a³⁺⁵ = a⁸

Por ejemplo:

2³. 2³ = 2³⁺³ = 2⁶ = 2 . 2 . 2 . 2 . 2 . 2 = 64
a¹⁵. a⁰ = a¹⁵⁺⁰ = a¹⁵
4^b. 4^c = 4^b+c

4) División de potencias de igual base

Para dividir potencias de la misma base, se restan los exponentes.

Por ejemplo:

a¹⁰ ÷ a³ = a^{10 - 3} = a⁷
b³ ÷ b⁴ = b^{3 - 4} = b ^-1 = 1 / b
x²³ / x¹³ = x ^{23 - 13} = x¹⁰

Todo número con exponente negativo es igual a su inverso con exponente positivo, como mostramos a continuación:

Otra forma de entender la división de potencias es eliminando términos comunes en el numerador y denominador, como, por ejemplo:

5) Ley de la uniformidad

Si los dos miembros de una igualdad se elevan a la misma potencia, resulta otra igualdad.

Por ejemplo:

a = 3
⇒ a² = 3² ⇒ a² = 9
⇒ a³ = 3³ ⇒ a³ = 27

6) Potencia de un producto

También se conoce como ley distributiva de la potenciación con respecto de la multiplicación. Esta ley establece que la multiplicación (a.b.c) elevada a la n (enésima potencia) es igual a cada uno de los factores elevado a esa potencia y luego multiplicado.

Por ejemplo:

Esto lo podemos demostrar de la siguiente manera:

Por ejemplo:

(2 x 3 )³ = 2³ x 3³ = (2.2.2) (3.3.3) = 8 x 27 = 216
(3ab)² = 3². a² . b² = 9 a²b²

7) Potencia de una fracción

También se conoce como ley distributiva de la potenciación respecto de la división exacta. Para elevar una fracción a una potencia, se elevan su numerador y denominador a dicha potencia de la siguiente forma:

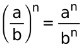
Por ejemplo:

En el caso de una fracción mixta, se transforma el número a fracción:

8) Potencia de una potencia

Si multiplicamos potencias de igual base e igual exponente tendremos una potencia de otra potencia:

a^m . a^m . a^m multiplicada n veces = (a^m)ⁿ = a^{m . n}

b³. b³ . b³= (b³)³ = b ^{3.x 3} = b⁹

Para resolver la potencia de una potencia, dejamos la misma base y multiplicamos los exponentes:

(2⁴)² = 2^{4 x 2} = 2⁸ = 256

9) Ley de monotonía

Cuando los dos miembros de una desigualdad son mayores que cero y se elevan a una misma potencia diferente de cero, resulta una desigualdad del mismo sentido.

Por ejemplo:

5 > 3
⇒ 5² > 3² ⇒ 25 > 9
⇒ 5³ > 3³ ⇒ 125 > 27

Vea también:

• Notación científica
• Jerarquía de operaciones.

Ejercicios (con soluciones)

1. Escribir las siguientes expresiones en forma de potencia única:

2. Hallar el valor de:

3. ¿Qué diferencia existe entre el cubo del doble de 2 y el doble del cubo de 2?

Vea también:

• Ley de los signos
• Factorización
• Ejercicios de productos notables
• Ejercicios de notación científica

Compartir

Revisado por Silvia Pina-Romero

Licenciada en Matemáticas por la Universidad Nacional Autónoma de México (2007) y doctora en Matemáticas por la Universidad de Manchester (2012).