El mínimo común múltiplo de 2 o más números (abreviado como mcm), es aquel número que es múltiplo de cada uno de los números y que, además, de todos los múltiplos en común, es el más pequeño.
Para sacar el mínimo común múltiplo de dos números puedes utilizar dos métodos:
1) Lista de múltiplos
Este método consiste en hacer una lista de sus múltiplos y encontrar al menor en común.
Supongamos que quieres obtener al mínimo común múltiplo de 6 y 8.
Obtenemos los primeros múltiplos de 6 haciendo la multiplicación de 6 por 1, 2, 3, 4, 5, 6, 7, 8, 9, …
6-12-18-24-30-36-42-48-54-...
Repetimos el procedimiento para calcular los múltiplos de 8
8-16-24-32-40-48-56-64-...
En esta lista hay elementos compartidos: el 24 y el 48. Si continúas la lista encontrarás más. De ellos el menor es 24, por tanto, el mcm es 24.
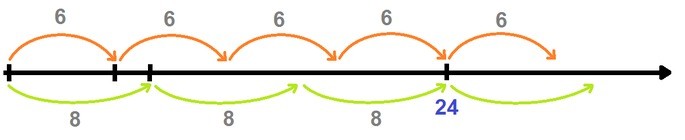
Esquemáticamente, así se ven los múltiplos de 6 y 8, y el mínimo común múltiplo
2) Descomposición en factores primos
Para este método debemos encontrar los números primos cuya multiplicación genera cada uno de los números.
A continuación se muestra una tabla con los números primos menores a 100:
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 |
El procedimiento paso a paso es el siguiente. Escribimos los dos números que vamos a descomponer seguidos de una línea vertical al lado derecho. Los factores los vamos a poner del otro lado de la línea.
Tomamos el primer número de la lista de primos y comprobamos si este divide a alguno de los dos que acabamos de escribir. Si esto sucede, lo escribimos a la derecha de la línea. En este caso, 2 divide a 6 y divide a 8 por lo que escribimos:
Debajo de 6 y 8, escribimos el resultado de dividir a cada número entre el factor del lado derecho.
Repetimos el procedimiento para los dos números que acabamos de obtener. Ahora sucede que 2 divide a 4 pero no a 3 (con que divida a uno de los números, se escribe como factor).
Debajo del 4 se escribe el resultado de dividir 4 entre 2, y el 3 se copia tal cual.
Volvemos a hacer el procedimiento, como 2 divide a 2, lo colocamos a la derecha.
Escribimos el resultado de dividir 2 entre 2 debajo del 2, y copiamos el 3.
Ahora observamos que el 2 ya no divide a ninguno de los números de la última fila, así que nos movemos al siguiente número de la tabla de primos: 3.
Cómo el 3 sí divide a uno de los últimos números, lo escribimos del lado derecho.
En la siguiente línea ponemos el resultado de dividir 3 entre 3 y el 1 que ya teníamos.
Ahora que todos los números de la última fila son 1, hemos terminado la descomposición.
Para encontrar el mcm, ahora debes multiplicar todos los factores del lado derecho. Es decir, mcm = 2 x 2 x 2 x 3 = 24.
Ejemplos
1. Calculemos el mínimo común múltiplo de 12 y 9
Ahora multiplicamos 2 x 2 x 3 x 3 x 3 = 108. Así que el mínimo común múltiplo es 108
2. Encuentra el mínimo común múltiplo de 5, 8 y 10
Multiplicamos 2 x 2 x 2 x 5 = 40. El mcm de 5, 8 y 10 es 40.
Problemas (con respuesta)
1. En una fila de 100 personas, Lucia reparte una estampa azul a la persona en la posición 9 y luego cada 9 personas, es decir a la persona 18, 27, etc. En la misma fila, Sara reparte una estampa amarilla a la persona que está en la posición 15, y luego otra a cada 15 personas. ¿En cuál posición está la primera persona que recibirá ambas estampas?
2. ¿Cuál es el denominador común más pequeño que permitiría sumar las fracciones 2/7, 1/4 y 2/12?
3. Dos llaves de agua gotean a diferentes intervalos, la primera deja salir una gota cada 10 segundos, la segunda cada 18 segundos. Si al inicio las dos gotean al mismo tiempo, ¿después de cuántos segundos volverán a coincidir?
Vea también: