Una función, en matemáticas, es una relación entre los elementos de dos conjuntos.
Por ejemplo, piensa en el conjunto de actores de una película y en el conjunto de personajes de la misma película, si ocurre que a cada actor le asignan un único personaje, entonces podemos decir que tenemos una función entre los actores y los personajes.
Lo que hace la función es asignar a cada actor, el personaje que le corresponde.
Esquemáticamente, podemos representar la función anterior de la siguiente manera:

En color rojo representamos al conjunto de actores, y en verde al de personajes. Las flechas que unen a los actores con su personaje, simbolizan la función. Al conjunto en rojo le llamamos dominio y al verde contradominio o imagen.
Otro ejemplo de función es la que asigna a la medida de un lado de un cuadrado, la medida del área de éste cuadrado.
En la siguiente tabla puedes ver algunas medidas de un lado de un cuadrado, y su correspondiente área.
| Lado de un cuadrado | Área de mismo cuadrado |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
La manera más frecuente de denotar una función es utilizando lenguaje algebraico para describir cómo se hace la asignación entre los elementos de los conjuntos. A estas funciones se les conoce como funciones algebraicas.
La función del ejemplo de la tabla de arriba, en lenguaje algebraico se escribe como:
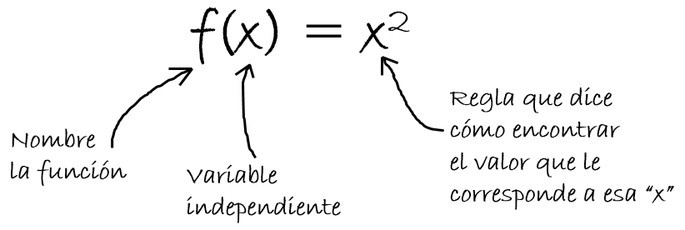
Tipos de funciones según su gráfica
Las funciones se pueden clasificar de acuerdo a diferentes características. A veces les llaman tipos de funciones aunque se trata, solamente, de una clasificación dentro de todas las clasificaciones posibles.
Una manera frecuente de clasificarlas es de acuerdo a su gráfica.
La gráfica es la colección de parejas de puntos (x,y) situados en una plano con ejes coordenados. Para el ejemplo f(x) = x2, en el que "x" representa una medida del lado de un cuadrado, y su correspondiente "y" es el área, la gráfica es la siguiente:

A continuación te mostraremos algunos tipos de funciones y sus gráficas:
Función trigonométrica
Por ejemplo, f(x) = sen(x).
La expresión sen(x) se lee como "seno de x".
Las funciones trigonométricas son una clase especial de funciones en las que la variable independiente es la medida de un ángulo. La función asigna a este ángulo una razón entre los catetos y la hipotenusa de un triángulo.
Otras funciones trigonométricas son: coseno, tangente, cotangente, secante y cosecante.
La que sigue es la gráfica de f(x) = sen(x).
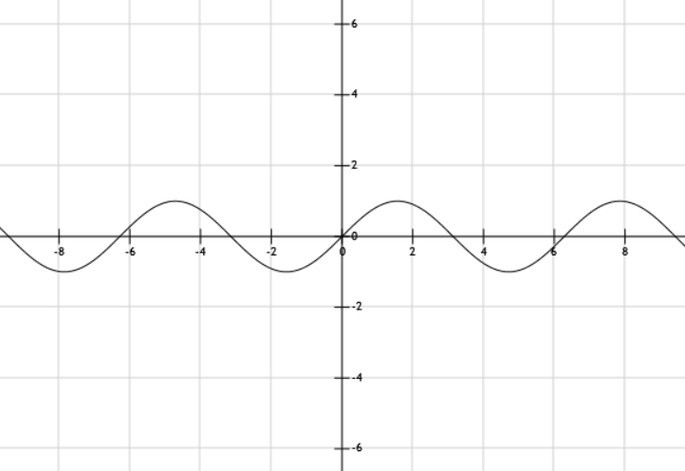
Vea también Funciones trigonométricas.
Función constante
Su forma general es f(x) = k, dónde k es un numero cualquiera fijo, es decir, a toda "x", independientemente de su valor, se le asigna el mismo valor de k.
En el ejemplo que sigue el valor de k es 6.
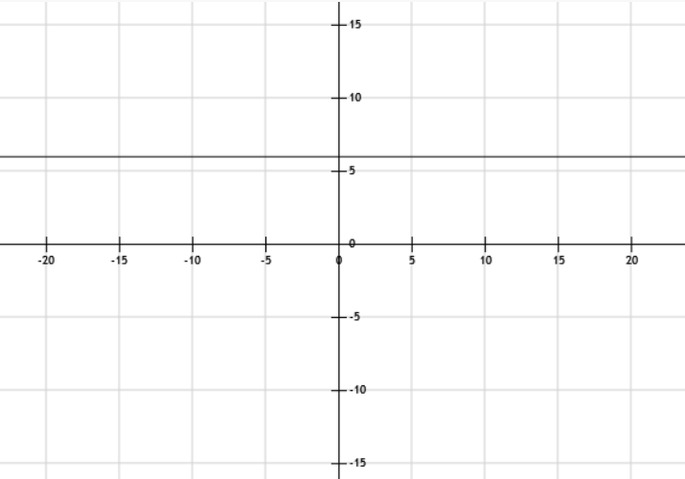
Función lineal
Se suele escribir como f(x) = ax + b, donde a y b son números fijos. La gráfica de estas funciones son siempre lineas rectas, su posición y dirección dependen de los valores de a y b.
Para este ejemplo a = 1 y b = -5.
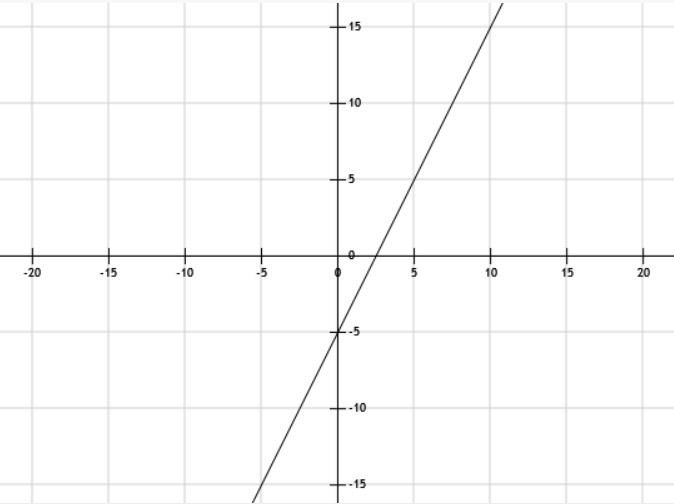
Función cuadrática
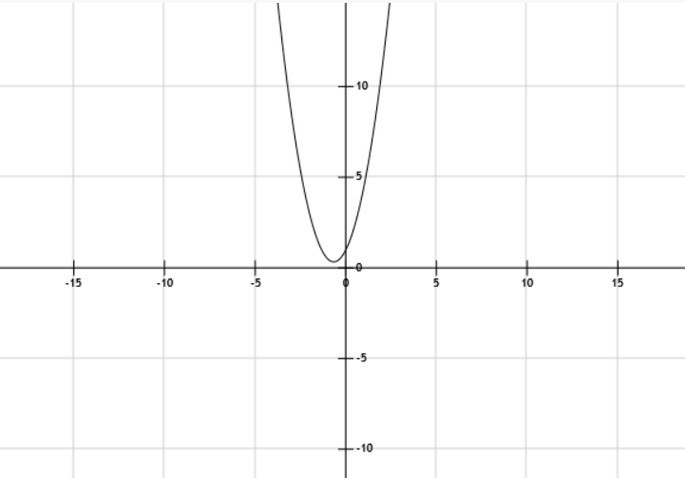
Se suele ver como f(x) = ax2 +bx +c, dónde a, b y c son números fijos. La gráficas de funciones cuadráticas se llaman parábolas. Pueden abrir hacia arriba o hacia abajo, estar desplazadas a la derecha o izquierda y abrirse de manera más rápida de acuerdo a los valores de a, b y c.
En este ejemplo a= 1.5, b=2 y c=1
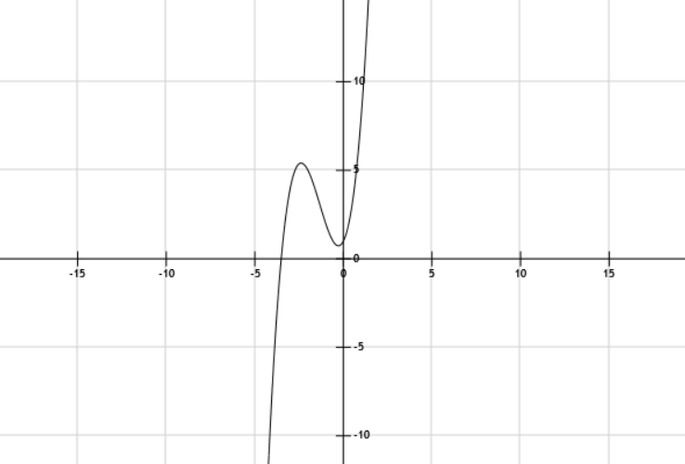
Función cúbica
Su forma general es f(x) = ax3 +bx2 +cx +d. De acuerdo al valor de a, b, c y d, la gráfica puede cambiar de posición, crecer más o menos rápido y distanciar o acercar su máximo y mínimo local.
Para esta gráfica se usaron los valores a = 1, b= 4, c = 2 y d = 1.
Función polinomial
Su ecuación general es: f(x) = anxn + an-1xn-1 + ...+ a2x2+ ax+ a0
La gráfica de una función polinomial, dependiendo de los valores que tome n y todos los coeficientes y constantes, puede tomar diferentes formas. Por esta razón no podemos hablar de una gráfica única, de hecho, las funciones anteriores (lineal, cuadrática y cúbica) son casos específicos de funciones polinomiales.
Función racional
Una función racional es un cociente de dos funciones polinomiales, o sea, algo de la forma f(x) = p(x) / q(x). Dependiendo de la forma particular de p(x) y q(x) la apariencia de la gráfica puede ser muy distinta, por lo que no se incluye una gráfica aquí.
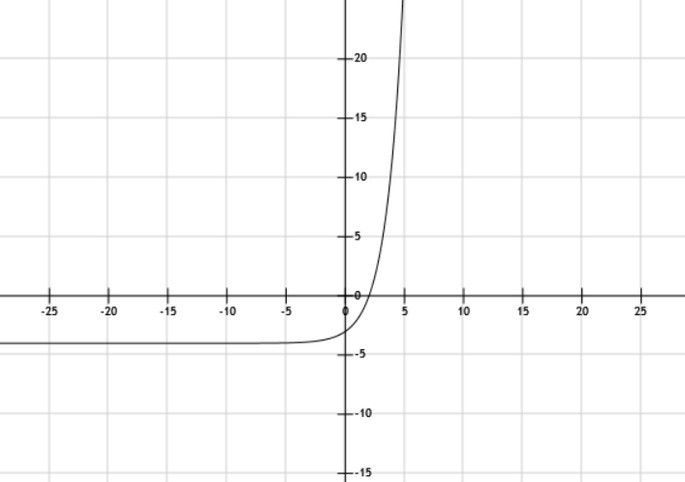
Función potencia
Suele verse como f(x)= kx + c, de acuerdo al valor de k, x y c la gráfica puede crecer más o menos rápido, verse invertida horizontalmente y desplazada a la derecha o izquierda.
En este caso k=2 y c = -4
Ver también Plano Cartesiano
Cómo se hace la gráfica de una función
Para dibujar la gráfica de una función algebraica dada, por ejemplo, f(x) = x3, debes seguir los siguientes pasos.
Paso 1: Determina cuál es el dominio y el contradominio de la función.
En el ejemplo f(x) = x3, tanto "x" como "y" pueden tomar cualquier valor de la recta real, de manera que el dominio y el contradominio son los números reales.
Paso 2: Utilizando la información del paso anterior, dibuja los ejes coordenados que te sean útiles.
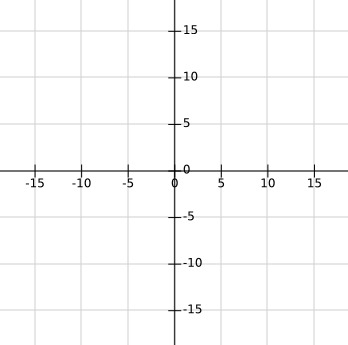
Paso 3: Elabora una tabla donde asignes algunos valores arbitrarios para "x" y calcules su correspondiente "y" siguiendo la regla de que indica f(x). Puedes elegir cualquier x del dominio, pero es útil para su graficación que se pueden apreciar en los ejes que dibujaste en el paso anterior.
| x | y |
|---|---|
| -2 | -8 |
| -1.5 | -3.37 |
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 1.5 | 3.37 |
| 2 | 8 |
Paso 4: Marca las parejas de puntos que encontraste en el paso anterior en el plano cartesiano que dibujaste en el paso 2.
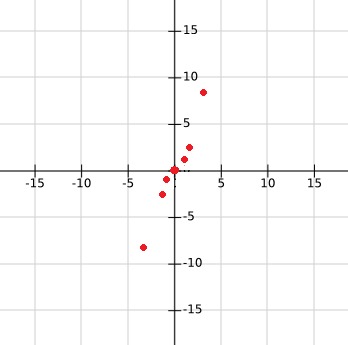
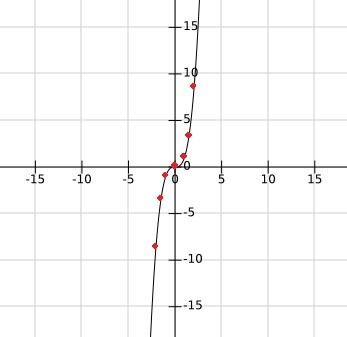
Paso 5: Une suavemente los puntos que marcaste en el paso anterior
Te puede interesar: